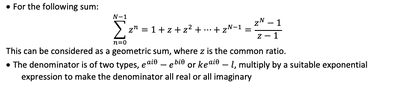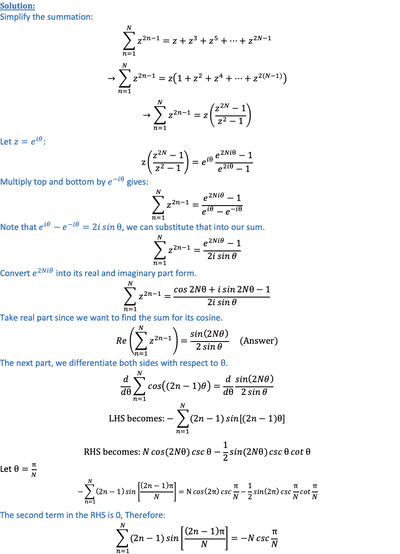Complex Numbers in Further Mathematics

- 复数的定义与表示



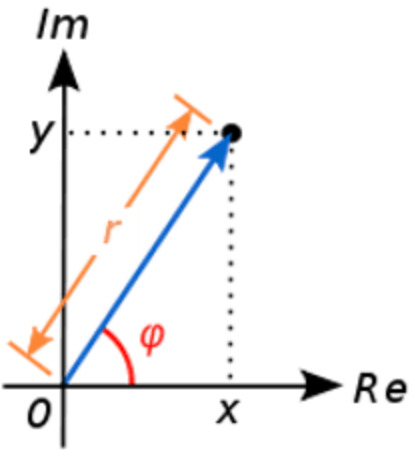
2. De Moivre公式
• 用于复数幂运算和开方:
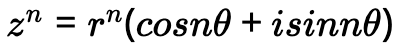
3. 复数方程求解(幂与开方)

4.复数相关经典题型
题型 1:复数方程解法
例题:解复数方程 z^4 = 16 。

5.cos和sin的多次方


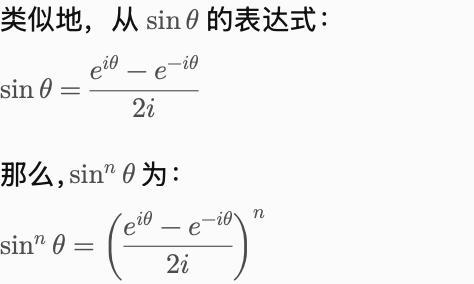
Example
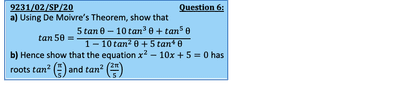
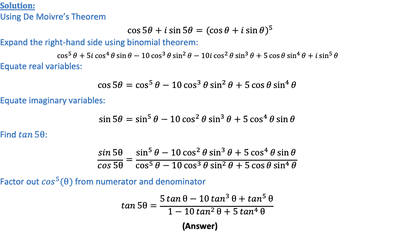

6.复数求和
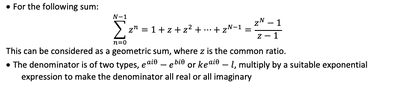

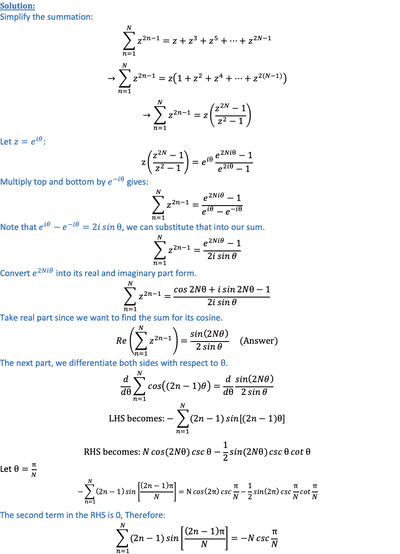





2. De Moivre公式
• 用于复数幂运算和开方:
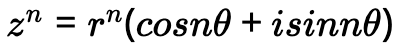
3. 复数方程求解(幂与开方)

4.复数相关经典题型
题型 1:复数方程解法
例题:解复数方程 z^4 = 16 。

5.cos和sin的多次方


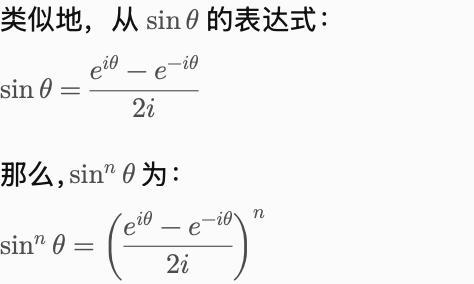
Example
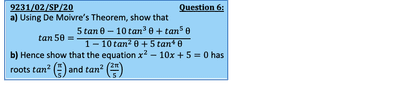
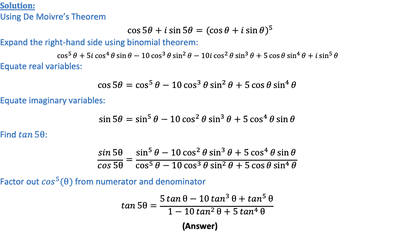

6.复数求和