Differentiation and Differential Equations

AS-Level 数学 | 微分与微分方程考点总结

在 AS-Level 数学中，微分（Differentiation）和微分方程（Differential Equations）是重要的内容，广泛应用于函数分析、物理建模和经济学问题中。本文将总结考点、常见公式以及解题技巧，帮助大家更好地掌握这部分知识。

一、微分（Differentiation）

1. 微分的基本概念

微分是研究函数变化率的工具，用于求导数（Derivative）。

• 导数的定义

导数表示函数在某点的瞬时变化率。

• 几何意义

导数表示函数曲线在点  x  处的切线斜率。

2. 基本求导公式

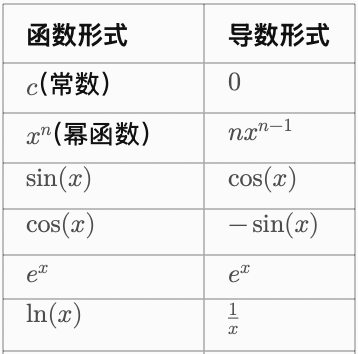
3. 微分法则

1. 加法与减法法则

2. 乘积法则

3. 商法则

4. 链式法则

5.内导外导法则

简单来说，就是：

1. 外导：先对外层函数  f(u)  求导（把内层  g(x)  当作整体）。

2. 内导：再对内层函数  g(x)  求导。

3. 内外相乘：将两者相乘得到结果。

二、微分方程（Differential Equations）

1. 微分方程的概念

微分方程是包含未知函数及其导数的方程

在 A-Level 中，主要考察一阶和二阶微分方程。

2. 常见微分方程的解法

变量分离法

适用于可分离变量的微分方程：

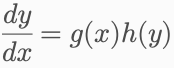
解法：

1. 将方程写为

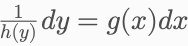
2. 对两边积分：

三、A-Level 典型考题与解法

1. 基本求导题

2. 微分方程求解题

微分和微分方程是 A-Level 数学的重点考点，理解基本公式和解题方法是关键。 以上是基本解题思路，多多刷题了解不同题型和考点，微分更讲究熟练度，可以尝试练习以下题目

希望这篇文章对你有所帮助！在后续学习中，结合实际问题理解这些知识点，将会更加得心应手。