Data Representation

Binary – base two number system based on the values 0 and 1 only.

Prefixes

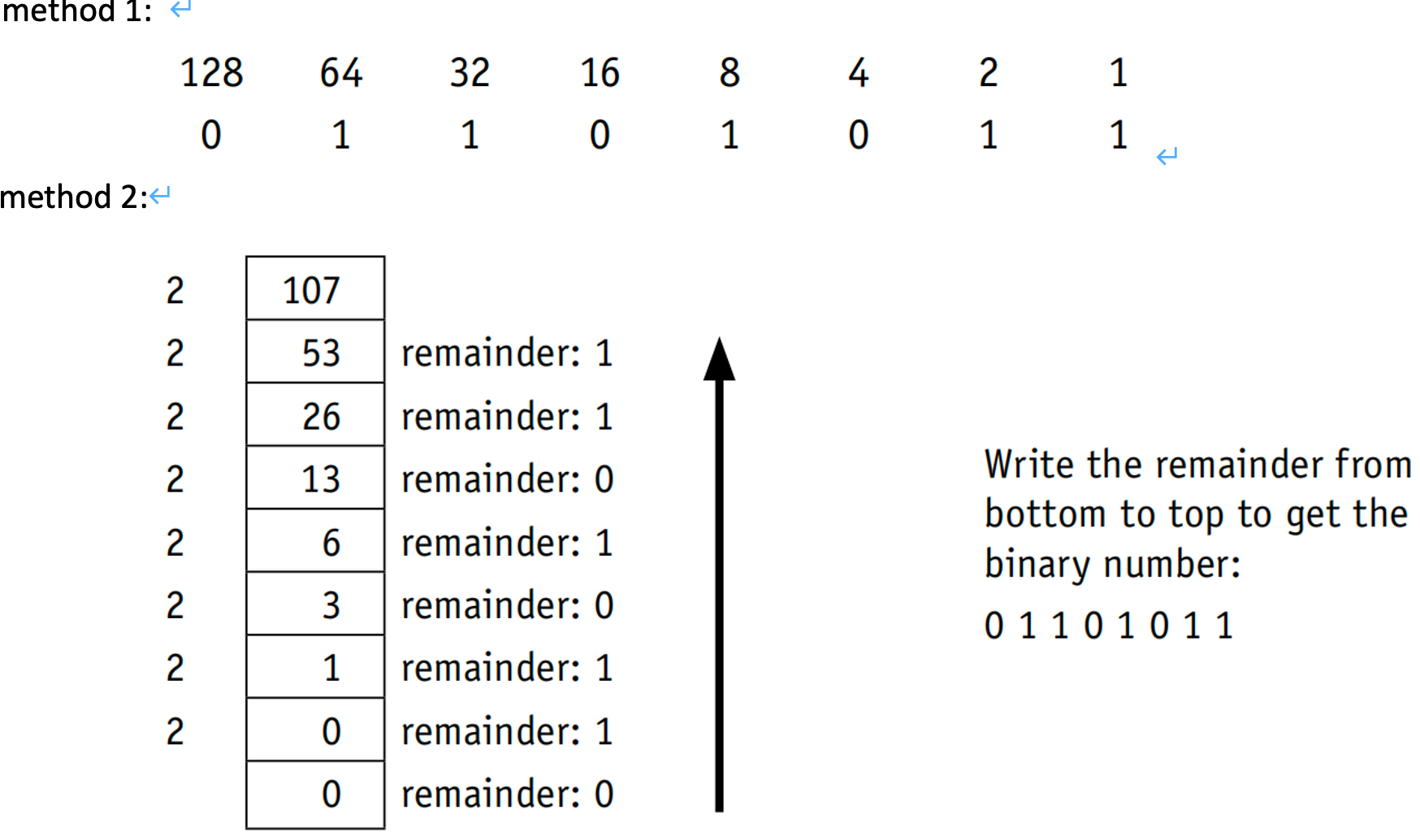
Converting from binary to denary and from denary to binary

Example：

a)   binary: 1 1 1 0 1 1 1 0

denary: 128 + 64 + 32 + 8 + 4 + 2 = 238 (denary)

b)   the conversion of the denary number, 107, into binary

Binary addition and subtraction

one’s complement - each digit in the binary number is inverted (in other words, 0 becomes 1 and 1 becomes 0).

For example, 0 1 0 1 1 0 1 0 (denary value 90) becomes 1 0 1 0 0 1 0 1 (denary value −90).

 two’s complement - each digit in the binary number is inverted and a ‘1’ is added to the right-most bit. (left-most bit, most significant bit, MSB)

For example, 0 1 0 1 1 0 1 0 (denary value 90) becomes:

1 0 1 0 0 1 0 1 + 1 = 1 0 1 0 0 1 1 0

(since 1 + 1 = 0, a carry of 1) = denary value −90

Overflow – the result of carrying out a calculation which produces a value too large for the computer’s allocated word size.

Hexadecimal number system

a system based on 16 different digits, the numbers 0 to 9 and the letters A to F, four binary digits are equivalent to each hexadecimal digit.

Practical applications: 

1.Defining colours in HTML  2.Debugging via memory dumps

3.Defining Media Access Control (MAC) addresses

4.Assembly languages and machine code     5.IP addresses(IPv6)

Binary-coded decimal (BCD) system

binary-coded decimal (BCD) system uses a 4-bit code to represent each denary digit

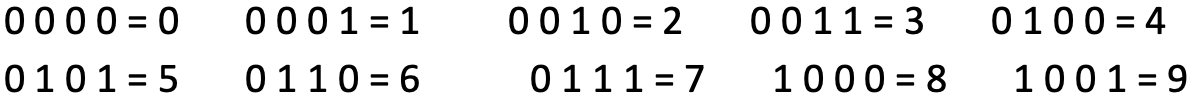
Exercise 1

State two benefits of using Binary Coded Decimal (BCD) to represent values.[2]

 Answer:

• straightforward to convert to / from BCD and denary

• ... so it is less complex to encode and decode for programmers

• easier for digital equipment use BCD to display output information

• can represent monetary货币 values exactly

Exercise 2

Identify one practical application of BCD and justify why BCD is used in this application.[2]

Character Set

ASCII codes and Unicodes

The standard ASCII code character set consists of 7-bit codes (0 to 127 denary or 0 to 7F in hexadecimal)

this represents the letters, numbers and characters found on a standard keyboard together with 32 control codes.

Extended ASCII uses 8-bit codes (128 to 255 in denary or 80 to FF in hex). This allows for non-English characters and for drawing characters to be included.

Unicode allows characters in a code form to represent all languages of the world (Huffman coding)

Exercise:

Answer:

Similarity (max 1):

• both can use 8 bits        • both represent each character using a unique code

• Unicode will contain all the characters that ASCII contains // ASCII is a subset of Unicode

Differences (max 2):

• Unicode can go up to 32 bits per character whereas ASCII is 7 or 8 bits

•Unicode can represent a wider range of characters than ASCII

• different languages are represented using Unicode, ASCII is only for one language