Integration

积分是微积分中的重要部分，它是微分的逆运算。在A-level数学中，积分主要分为不定积分（Indefinite Integration）和定积分（Definite Integration）

1. 不定积分

不定积分给出函数的原函数形式，并包含一个常数项 C（积分常数）。

基本积分公式

1. 幂函数积分：

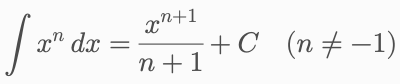
2. 指数函数积分：

3. 三角函数积分：

4. 复合函数积分（代换法的基础）：

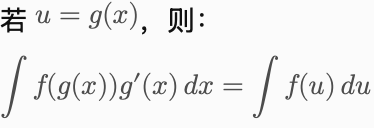
2. 定积分

定积分用于计算曲线下的面积，其结果为一个具体值，没有积分常数 C。

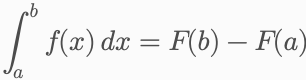
其中，F(x) 是 f(x) 的一个原函数

几何意义

• 定积分表示曲线 y = f(x) 与 x-轴之间从 x = a 到 x = b 的净面积（上方为正，下方为负）。

3. 常用积分技巧

1. 分解积分

若函数是多项式或加减形式：

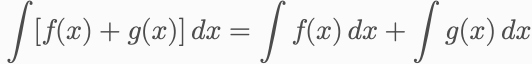
2. 代换法

用于积分中含有复杂复合函数的情况：

1. 设 u = g(x)，计算 du = g'(x) dx。

2. 将积分转化为关于 u 的表达式并计算。

3. 换回原变量 x。

Example：

3. 分部积分法

用于两个函数的乘积积分：

选择 u 和 dv 的标准为“LIATE”原则（Logarithmic, Inverse, Algebraic, Trigonometric, Exponential）。

4. 常见积分题型与解答

例题 1：简单多项式积分

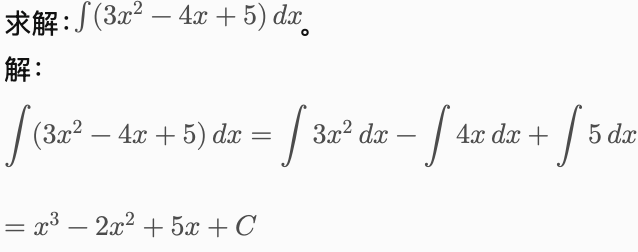
例题 2：定积分求面积

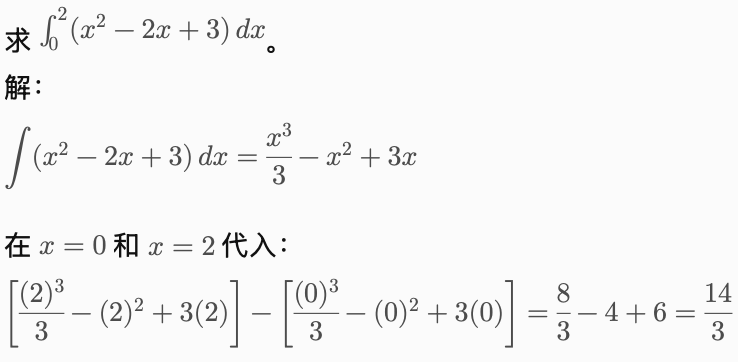
例题 3：三角函数积分

例题 4：分部积分

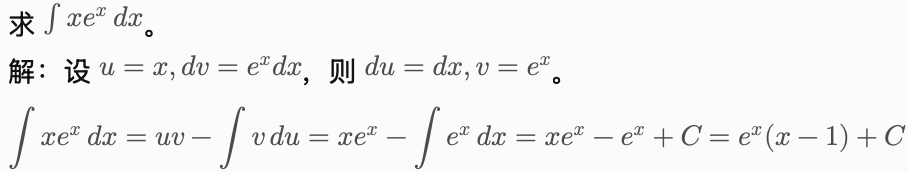
和积分一样，微分也需要大量练习提升熟练度，可以试试以下题目，希望这篇文章能对你有所帮助。